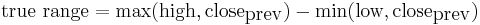Average True Range

Average True Range (ATR) is a technical analysis volatility indicator originally developed by J. Welles Wilder, Jr. for commodities[1]. The indicator does not provide an indication of price trend, simply the degree of price volatility.[2] The average true range is an N-day exponential moving average of the true range values. Wilder recommended a 14-period smoothing. [3]

Contents

Calculation

The range of a day's trading is simply 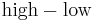\mbox{high} - \mbox{low}. The true range extends it to yesterday's closing price if it was outside of today's range.

\mbox{true range} = {\max(\mbox{high}, \mbox{close}_\mbox{prev}) - \min(\mbox{low}, \mbox{close}_\mbox{prev})}\,

The true range is the largest of the:

The idea of ranges is that they show the commitment or enthusiasm of traders. Large or increasing ranges suggest traders prepared to continue to bid up or sell down a stock through the course of the day. Decreasing range suggests waning interest.

Applicability to futures contracts vs. stocks

Since true range and ATR are calculated by subtracting prices, the volatility they compute does not change when historical prices are backadjusted by adding or subtracting a constant to every price. Backadjustments are often employed when splicing together individual monthly futures contracts to form a continuous futures contract spanning a long period of time. However the standard procedures used to compute volatility of stock prices, such as the standard deviation of logarithmic price ratios, are not invariant to (addition of a constant). Thus futures traders and analysts typically use one method (ATR) to calculate volatility, while stock traders and analysts typically use another (SD of log price ratios).

References

  1. ^ J. Welles Wilder, Jr. (June 1978). New Concepts in Technical Trading Systems. Greensboro, NC: Trend Research. ISBN 978-0894590276. 
  2. ^ ATR Definition - investopedia.com
  3. ^ This is by his reckoning of EMA periods, meaning an α=2/(1+14)=0.1333.

External links

Concepts
Charts
Patterns
Indicators
accumulation/distribution index · Money flow index (MFI) · On-balance volume (OBV) · Volume price trend (VPT) · Force index (FI) · Negative volume index (NVI) · Ease of movement · Put/call ratio (PCR)
Other